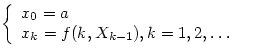назад

ЛАБОРАТОРНАЯ РАБОТА 7.
ПРОГРАММИРОВАНИЕ АЛГОРИТМОВ ПРИ ПОМОЩИ РЕКУРСИВНЫХ ПРОЦЕДУР И ФУНКЦИЙ

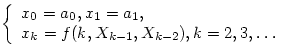
Цель работы: познакомиться с понятием "рекурсия" и особенностями рекурсивных процедур и функций языка программирования Pascal, закрепить практические навыки работы с системой TURBO Pascal на примере реализации алгоритмов при помощи рекурсивных процедур и функций.

 

[Оглавление]

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

 Рекурсия  (самоповторение) - действие, возвращающееся к "самому себе". Имеется два вида рекурсии: (1)  прямая рекурсия  означает, что процедура вызывает саму себя; (2) косвенная рекурсия означает, что одна процедура вызывает другую процедуру, а это в свою очередь прямо или косвенно приводит к вызову первоначальной процедуры.

Рекурсию следует использовать только тогда, когда задача легко поддается рекурсивному решению. Любая задача, которая может быть решена рекурсивно, также может быть решена и без рекурсии.

С понятием рекурсии тесно связано понятие "рекуррентная последовательность", вычисление n-го члена которой производится с помощью рекурсии. Определим это понятие: числовая последовательность {$Х_k$} называется  рекуррентной , если \begin{displaymath} \left\{ \begin{array} {ll} X_0=a_0,X_1=a_1,\ldots,X_{p-1}=a... 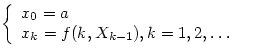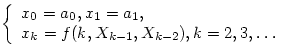...{k-1},X_{k-2},\ldots,X_{k-p}),k=p,p+1,\ldots&\end{array}\right.\end{displaymath}В частности, при p=1 $\left\{ \begin{array} {ll} x_0=a&\\ x_k=f(k,X_{k-1}),k=1,2,\ldots&\end{array}\right.$, при р=2:$\left\{ \begin{array} {ll} x_0=a_0,x_1=a_1,&\\ x_k=f(k,X_{k-1},X_{k-2}),k=2,3,\ldots&\end{array}\right.$

[Оглавление]

ДЕМОНСТРАЦИОННЫЕ ПРИМЕРЫ

Пример  Рекурсивное и нерекурсивное вычисление факториала натурального  числа  n. 

   PROGRAM Fact (Input,Output); {$N+ $E+} { Рекурсивное вычисление факториала }
      var  n: Integer;
   { ------------------------------------------------------------------------ }
   FUNCTION  RecursiveFact (n: Integer): Integer;
   BEGIN  { Рекурсивное вычисление факториала }
      If  n=0
         then RecursiveFact:=1
         else RecursiveFact:=n*RecursiveFact(n-1)
   END;
   { ------------------------------------------------ }
   FUNCTION  NonRecursiveFact (n: Integer): Integer;
      var  P: Integer;
   BEGIN { Вычисление факториала с использованием вместо рекурсии повторения  }
      P:=1;
      While  n>1  do  begin P:=n*P; n:=n-1 end;
      NonRecursiveFact:=P
   END;
   { ---- }
   BEGIN
      Write ('Введите натуральное число: '); ReadLn (n);
      Write ('Результат, вычисленный рекурсивно: '); WriteLn (RecursiveFact(n));
      Write ('Результат, вычисленный нерекурсивно: ');
      WriteLn (NonRecursiveFact(n))
   END.

Пример 2

 Рекурсивный и нерекурсивный поиск наибольшего общего делителя двух чисел. 

   PROGRAM  NOD (Input,Output);
      var  X,Y: Integer;
   { ------------------------------------------------ }
   FUNCTION  RecursiveNOD (n,m: Integer): Integer;
   BEGIN     { Рекурсивное вычисление НОД чисел n и m }
      If  n=m
        then  RecursiveNOD:=n
        else  If  n>m
                then  RecursiveNOD:=RecursiveNOD (n-m,m)
                else  RecursiveNOD:=RecursiveNOD (n,m-n)
   END;
   { ------------------------------------------------ }
   FUNCTION  NonRecursiveNOD (n,m: Integer): Integer;
   BEGIN    { Алгоритм, использующий вместо рекурсии повторение }
      While  n<>m  do
         If  n>m
            then  n:=n-m
            else  m:=m-n;
      NonRecursiveNOD:=n
   END;
   { ---- }
   BEGIN
      Write ('Введите два целых числа, отличных от 0: '); Read (X); ReadLn (Y);
      Write ('Результат, полученный рекурсивно: ');
      WriteLn (RecursiveNOD(Abs(X),Abs(Y)));
      Write ('Результат, полученный нерекурсивно: ');
      WriteLn (NonRecursiveNOD(Abs(X),Abs(Y)))
   END.

 

[Оглавление]

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1.

Написать программу вычисления P по формуле: 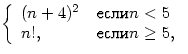$\left\{ \begin{array} {ll} (n+4)^2& если n<5 \\ n!,&если n\geq 5,\end{array}\right.$где n - заданное натуральное число.

2.

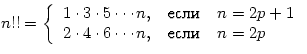
Написать программу вычисления $\sum_{k=1}^{n}{(-1)^{k}\cdot k!!}$, где $n!!= \left\{ \begin{array} {lll} 1\cdot 3\cdot 5\cdots n ,& если & n=2p+1 \\ 2\cdot 4\cdot 6\cdots n ,& если & n=2p\end{array}\right.$

3.

Дано натуральное число n. Найти (2n)! и 2n!. Использовать рекурсивную функцию вычисления факториала.

4.

Даны натуральные числа n,m. Найти НОД(n,m). Использовать рекурсивную функцию вычисления НОД, основанную на соотношении НОД (n,m)=НОД (m,r), где r - остаток от деления n на m.

5.

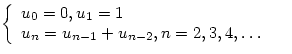Числа Фибоначчи $u_0,u_1,u_2,\ldots$определяются следующим образом: $\left\{ \begin{array} {ll} u_0=0,u_1=1&\\ u_n=u_{n-1}+u_{n-2},n=2,3,4,\ldots &\end{array}\right.$Проверить на нескольких примерах, будет ли $u_{5k},k=1,2,\ldots,$делиться на 5.

6.

Даны неотрицательные целые числа n и m. Вычислить функцию Аккермана: 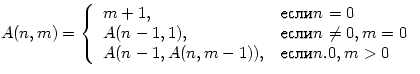$A(n,m)=\left\{ \begin{array} {ll} m+1,&если n=0\\ A(n-1,1),&если n\ne0,m=0\\ A(n-1,A(n,m-1)),&если n.0,m\gt\end{array}\right.$
Приведем некоторые тестовые примеры:$A(1,b)=b+2,A(2,b)=2^b+3,A(3,b)=2^{b+3}-3.$

7.

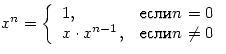
Описать рекурсивную функцию  Stepen(x,n) от вещественного x и натурального n, вычисляющую (через умножение) величину $x^n$, и использовать ee для вычисления $2^k+k^3$Величину $x^n$вычислять по формуле: $x^n=\left\{ \begin{array} {ll} 1,&если n=0\\ x\cdot x^{n-1},&если n\ne 0\end{array}\right.$

8.

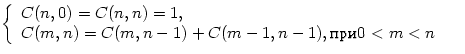
Описать рекурсивную функцию C(m,n)$(0\leqslant m\leqslant n)$ для вычисления биноминального коэффициента по формуле: $\left\{ \begin{array} {ll} C(n,0)=C(n,n)=1,&\\ C(m,n)=C(m,n-1)+C(m-1,n-1), при 0<m<n&\end{array}\right.$

9.

Описать рекурсивную функцию, позволяющую вычислить 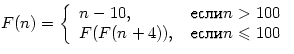$F(n)=\left\{ \begin{array} {ll} n-10,&если n\gt 100\\ F(F(n+4)),&если n\leqslant 100\end{array}\right.$
Какие возможные значения принимает эта функция?

10.

Описать рекурсивную функцию, позволяющую вычислить 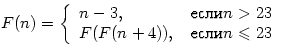$F(n)=\left\{ \begin{array} {ll} n-3,&если n\gt 23\\ F(F(n+4)),&если n\leqslant 23\end{array}\right.$

11.

Описать рекурсивную функцию  Strannost, определенную на множестве положительных целых чисел следующим образом: 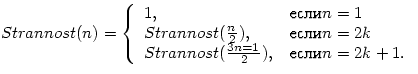$Strannost(n)=\left\{ \begin{array} {ll} 1,&если n=1\\ Strannost(\frac{n}{2}),&если n=2k\\ Strannost(\frac{3n=1}{2}),&если n=2k+1.\end{array}\right.$

12.

Написать рекурсивную процедуру, при выполнении которой на экран будет выводиться отрезок натурального ряда чисел.

13.

Найти все трехзначные числа, представимые в виде сумм факториалов своих цифр. Использовать рекурсивную функцию вычисления n!.

14.

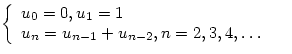
Числа Фибоначчи $u_0,u_1,u_2,\ldots$определяются следующим образом: $\left\{ \begin{array} {ll} u_0=0,u_1=1&\\ u_n=u_{n-1}+u_{n-2},n=2,3,4,\ldots &\end{array}\right.$
Написать программу вычисления первого числа Фибоначчи, большего m (m>1), включающую рекурсивную функцию, которая основана на непосредственном использовании соотношения $ u_n=u_{n-1}+u_{n-2}$

15.

Определить число, получаемое выписыванием в обратном порядке цифр заданного натурального числа (использовать рекурсивную функцию).

16.

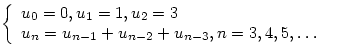
Числа Фибоначчи второго порядка $u_0,u_1,u_2,\ldots$определяются следующим образом: $\left\{ \begin{array} {ll} u_0=0,u_1=1,u_2=3&\\ u_n=u_{n-1}+u_{n-2}+u_{n-3},n=3,4,5,\ldots &\end{array}\right.$
Написать программу вычисления $u_n$для данного неотрицательного целого n.

17.

Установить назначение следующей функции: 

   FUNCTION  SumOfDigits (n: Integer): Integer;
   BEGIN
      If  n=0
         then  SumOfDigits:=0
         else  SumOfDigits:=(n MOD 10)+SumOfDigits (n DIV 10)
   END;

18.

Установить назначение следующей функции: 

   FUNCTION  HiDigit (n: Integer): Integer;
   BEGIN
      If  n<10
         then  HiDigit:=n
         else  HiDigit:=HiDigit (n DIV 10)
   END;

19.

Пусть 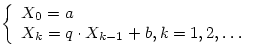$\left\{ \begin{array} {ll} X_0=a&\\ X_k=q\cdot X_{k-1}+b,k=1,2,\ldots &\end{array}\right.$Вычислить для заданного натурального n.

20.

Среди первых n+1 элементов последовательности 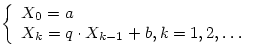$\left\{ \begin{array} {ll} X_0=a&\\ X_k=q\cdot X_{k-1}+b,k=1,2,\ldots &\end{array}\right.$
найти количество тех элементов, которые принадлежат интервалу (с,d). Предполагается, что $q \ne 0$.

21.

Задана рекуррентная последовательность 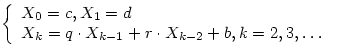$\left\{ \begin{array} {ll} X_0=c,X_1=d&\\ X_k=q\cdot X_{k-1}+r\cdot X_{k-2}+b,k=2,3,\ldots &\end{array}\right.$
Вычислить $X_n(n\geqslant 0)$. Считать $r\ne 0$.

22.

Числа Фибоначчи  определяются следующим образом: 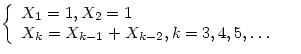$\left\{ \begin{array} {ll} X_1=1,X_2=1&\\ X_k=X_{k-1}+X_{k-2},k=3,4,5,\ldots &\end{array}\right.$
Найти номер первого числа Фибоначчи, которое больше h.

23.

Пусть $X_k=(-1)^{k+1}k!!,k=1,2,\ldots$Вычислить $X_k$для заданного натурального k.

24.

Найти (в выражении присутствуют ровно n радикалов): 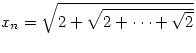$x_n=\sqrt{2+\sqrt{2+\cdots +\sqrt{2}}}$

25.

Вычислить, используя рекурсию (результат принадлежит Сринивазу Рамануджану). 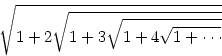\begin{displaymath} \sqrt{1+2\sqrt{1+3\sqrt{1+4\sqrt{1+\cdots}}}}\end{displaymath}Ответ: 3

26.

Вычислить, используя рекурсию (результат принадлежит Сринивазу Рамануджану) 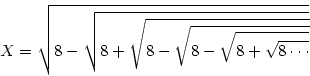\begin{displaymath} X=\sqrt{8-\sqrt{8+\sqrt{8-\sqrt{8-\sqrt{8+\sqrt{8\cdots }}}}}}\end{displaymath}где знаки перед корнями периодически повторяются группами по три: "-","+","-".Вывести уравнение, корнем которого является X.
Ответ: $X=1+2\sqrt{3}\sin {20}^o$

27.

Вычислить, используя рекурсию (результат принадлежит  Сринивазу Рамануджану) 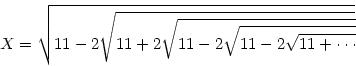\begin{displaymath} X=\sqrt{11-2\sqrt{11+2\sqrt{11-2\sqrt{11-2\sqrt{11+\cdots }}}}}\end{displaymath}где знаки перед корнями периодически повторяются группами по три: "-","+","-". Вывести уравнение, корнем которого является X.
Ответ:$X=1+4\sin{10}^o$

28.

Вычислить, используя рекурсию (результат принадлежит  Сринивазу Рамануджану) 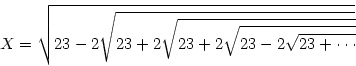\begin{displaymath} X=\sqrt{23-2\sqrt{23+2\sqrt{23+2\sqrt{23-2\sqrt{23+\cdots }}}}}\end{displaymath}где знаки перед корнями периодически повторяются группами по три: "-","+","+".Вывести уравнение, корнем которого является X.
Ответ: $X=1+4\sqrt{3} \sin{20}^o$

29.

Вычислить, используя рекурсию (результат принадлежит Сринивазу Рамануджану): 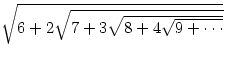$\sqrt{6+2\sqrt{7+3\sqrt{8+4\sqrt{9+\cdots }}}}$
Ответ:4

30.

Вычислить, используя рекурсию (результат принадлежит Сринивазу Рамануджану): 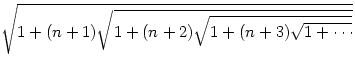$\sqrt{1+(n+1)\sqrt{1+(n+2)\sqrt{1+(n+3)\sqrt{1+\cdots }}}}$
(Ответ:)n+2

 

[Оглавление]

Hosted by uCoz